Mastering the Maximum Subarray Problem - Find the Contiguous Subarray with the Largest Sum

- Published on
The maximum subarray problem is a popular coding challenge that involves finding a contiguous subarray within a given integer array, which has the largest sum. This problem is often encountered in coding interviews and is an excellent opportunity to understand dynamic programming concepts. In this article, we'll dive into the maximum subarray problem, discuss the famous Kadane's algorithm for solving it, and walk through a step-by-step implementation using Python.
Problem Statement
Given an integer array, find the contiguous subarray with the largest sum.
Example:
Input: nums = [-2, 1, -3, 4, -1, 2, 1, -5, 4]
Output: 6
Explanation: The contiguous subarray with the largest sum is [4, -1, 2, 1], with a sum of 6.
Kadane's Algorithm
Kadane's algorithm is an efficient approach to solving the maximum subarray problem. The algorithm uses dynamic programming, where the solution to a problem depends on the solutions to smaller instances of the same problem. The main idea behind Kadane's algorithm is to keep track of the maximum sum ending at each position and update the global maximum sum whenever a new local maximum is found.
Python Implementation
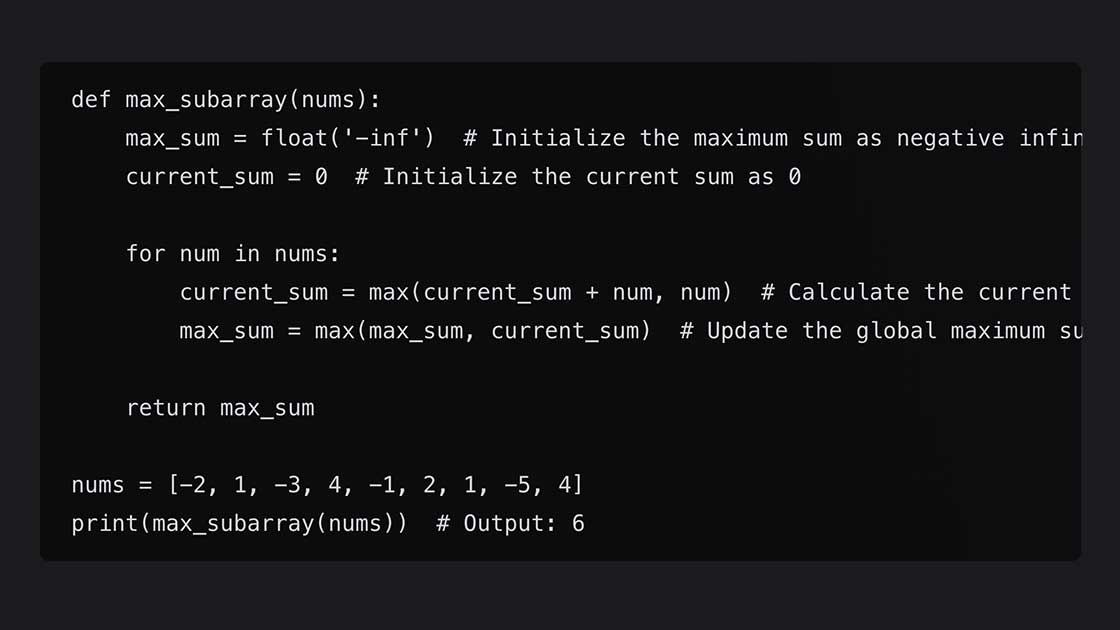
def max_subarray(nums):
max_sum = float('-inf') # Initialize the maximum sum as negative infinity
current_sum = 0 # Initialize the current sum as 0
for num in nums:
current_sum = max(current_sum + num, num) # Calculate the current sum ending at the current number
max_sum = max(max_sum, current_sum) # Update the global maximum sum if necessary
return max_sum
nums = [-2, 1, -3, 4, -1, 2, 1, -5, 4]
print(max_subarray(nums)) # Output: 6
Pros:
- Efficient solution with a time complexity of O(n)
- Introduces dynamic programming concepts
Cons:
- Requires a good understanding of dynamic programming for beginners
Hi there! Want to support my work?
The maximum subarray problem is an essential coding challenge that helps developers learn dynamic programming concepts and problem-solving strategies. By understanding the problem statement, grasping the core concepts of Kadane's algorithm, and practicing the implementation, you can enhance your programming skills and prepare for coding interviews or real-world applications. Keep practicing, and don't forget to apply dynamic programming techniques to other problems you encounter on your coding journey!